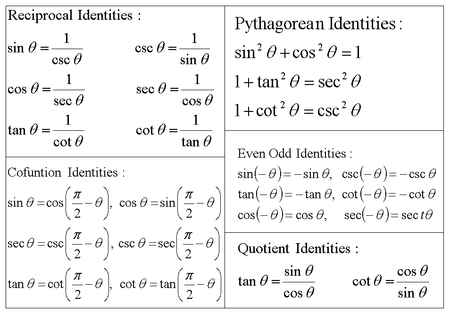
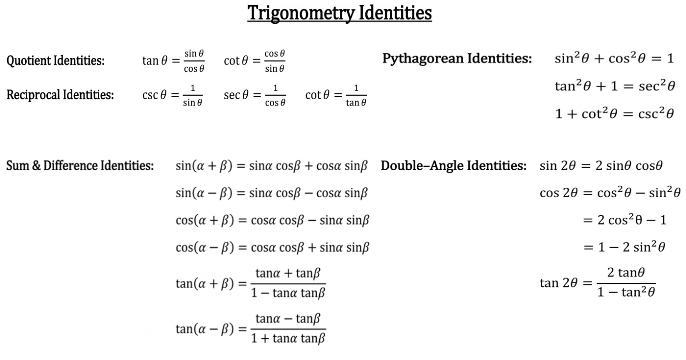
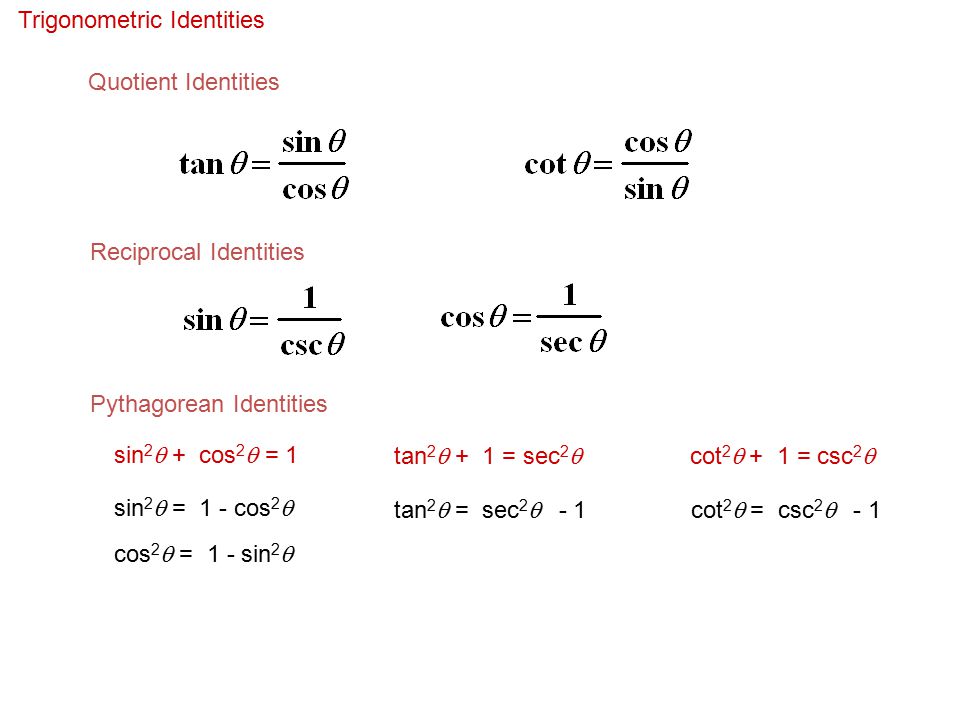
TRIGONOMETRIC IDENTITIES Reciprocal identities sinu= 1 cscu cosu= 1 secu tanu= 1 cotu cotu= 1 tanu cscu= 1 sinu secu= 1 cosu Pythagorean Identities sin 2ucos u= 1 1tan2 u= sec2 u 1cot2 u= csc2 u Quotient Identities tanu= sinu cosu cotu= cosu sinu CoFunction Identities sin(ˇ 2 u) = cosu cos ˇ 2 u) = sinu tan(ˇ 2 u) = cotu cot(ˇ 2 u) = tanu csc(ˇ 2 u) = secu sec(ˇ 2 u) = cscuDefinition of the Trig Functions Right triangle definition For this definition we assume that 0 2 pThe other four trigonometric functions (tan, cot, sec, csc) can be defined as quotients and reciprocals of sin and cos, except where zero occurs in the denominator It can be proved, for real arguments, that these definitions coincide with elementary geometric definitions if the argument is regarded as an angle given in radians
What Does It Mean To Prove A Trigonometric Identity Socratic
Trig identities for tan 2
Trig identities for tan 2-Hyperbolic Trig Identities is like trigonometric identities yet may contrast to it in specific terms The fundamental hyperbolic functions are hyperbola sin and hyperbola cosine from which the other trigonometric functions are inferred You can easily explore many other Trig Identities on this website So here we have given a Hyperbola diagram along these lines giving you thoughtList of trigonometric identities 2 Trigonometric functions The primary trigonometric functions are the sine and cosine of an angle These are sometimes abbreviated sin θ) and cos(θ), respectively, where θ is the angle, but the parentheses around the angle are often omitted, eg, sin θ and cos θ The tangent (tan) of an angle is the ratio of the sine to the cosine Finally, the



2
To determine the difference identity for tangent, use the fact that tan(−β) = −tanβ Example 1 Find the exact value of tan 75° Because 75° = 45° 30° Example 2 Verify that tan (180° − x) = −tan x Example 3 Verify that tan (180° x) = tan x Example 4 Verify that tan (360° − x) = − tan x The preceding three examples verify three formulas known as the reductionThe "big three" trigonometric identities are sin2 tcos2 t = 1 (1) sin(AB) = sinAcosB cosAsinB (2) cos(AB) = cosAcosB −sinAsinB (3) Using these we can derive many other identities Even if we commit the other useful identities to memory, these three will help be sure that our signs are correct, etc 2 Two more easy identities From equation (1) we can generate two more identitiesIntegral of tan^2(x) How to integrate it step by step!👋 Follow @integralsforyou on Instagram for a daily integral 😉📸 @integralsforyou https//wwwinstag
Using basic trig identities, we know tan(θ) can be converted to sin(θ)/ cos(θ), which makes everything sines and cosines $$1 − cos(2θ) = ({sin(θ)}/{cos(θ)}) sin(2θ)$$ Distribute the right side of the equation $$1 − cos(2θ) = 2sin^2(θ)$$ There are no more obvious steps we can take to transform the right side of the equation, so let's move to the left side We can use theTangent and cotangent identities Pythagorean identities Sum and difference formulas Doubleangle formulas Halfangle formulas Products as sums Sums as products A N IDENTITY IS AN EQUALITY that is true for any value of the variable (An equation is an equality that is true only for certain values of the variable) In algebra, for example, we have this identity (x 5)(x − 5) = x 2Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify Statistics Arithmetic Mean Geometric Mean Quadratic Mean Median Mode Order Minimum Maximum Probability MidRange Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
Get more lessons & courses at http//wwwmathtutordvdcomLearn the basic trigonometric identities that can be used to solve numerous types of problems in triA trigonometric equation is an equation that involves a trigonometric function or functions When we solve a trigonometric equation we find a value for the trigonometric function and then find the angle or angles that correspond to that particular trigonometric function 2 Some important identities derived from a rightangled triangleIdentities involving trig functions are listed below Pythagorean Identities sin 2 θ cos 2 θ = 1 tan 2 θ 1 = sec 2 θ cot 2 θ 1 = csc 2 θ Reciprocal Identities




Trigonometric Identities Proofs List Of Trig Identities




List Of Trigonometric Identities Wikipedia
1 Identities and FormulasWhat patterns are there in these expressionsThis page is about the trigonometric functions of sine, cosine and tangent (60°)=1/2 and sin(60°)=√3/2 as well as tan(45°)=1, but are 30, 45 and 60 the only angles up to 90° with a formula for their trig values?




How Do You Use The Fundamental Trigonometric Identities To Determine The Simplified Form Of The Expression Socratic




Integrate Sec 2x Method 2
Ranges of the Trig Functions 1 sin 1 1 cos 1 1 tan 1 csc 1 and csc 1 sec 1 and sec 1 1 cot 1 Periods of the Trig Functions The period of a function is the number, T, such that f ( T ) = f ( ) So, if !is a xed number and is any angle we have the following periods sin(!Sin θ = −3/5 and 3π/2 < θ < 2π Find tan 2θ answer choices 24/7 24/7 113/4 s Question 32 SURVEY 900 seconds Q Use a doubleangle or halfangle identity to find the exact value of each expression cos θ = 4/5 and 270° < θ < 360°Find sin 2θ answer choices 1/5 24/2524/2525/24 s Question 33 SURVEY 900 seconds Q expand cos(2θ) answer choices cos 2 θ• use trigonometric identities to combine trigonometric functions 36 HELM (08) Workbook 4 Trigonometry 1 Trigonometric identities An identity is a relation which is always true To emphasise this the symbol '≡' is often used rather than '=' For example, (x1)2 ≡ x2 2x1 (always true) but (x1)2 = 0 (only true for x = −1) Task (a) Using the exact values, evaluate sin2 θ




Integrate Tan 2x




Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions
Trigonometric identities are equalities involving trigonometric functions An example of a trigonometric identity is sin 2 θ cos 2 θ = 1 \sin^2 \theta \cos^2 \theta = 1 sin2 θcos2 θ = 1 In order to prove trigonometric identities, we generally use other known identities such as Pythagorean identitiesTrigonometric Identities Pythagoras's theorem sin2 cos2 = 1 (1) 1 cot2 = cosec2 (2) tan2 1 = sec2 (3) Note that (2) = (1)=sin 2 and (3) = (1)=cos Compoundangle formulae cos(A B) = cosAcosB sinAsinB (4) cos(A B) = cosAcosB sinAsinB (5) sin(A B) = sinAcosB cosAsinB (6) sin(A B) = sinAcosB cosAsinB (7) tan(A B) = tanA tanB 1 tanAtanB (8) tan(A B) = tanA tanB 1Identities expressing trig functions in terms of their complements cos t = sin(/2 – t) sin t = cos(/2 – t) cot t = tan(/2 – t) tan t = cot(/2 – t) csc t = sec(/2 – t) sec t = csc(/2 – t) Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2 while tangent



2




Summary Of Trigonometric Identities
Using Trig Identities to Solve a Quadratic in Sin x Category Mathematics In the first of this pair of Casio videos, the identity sin 2 x cos 2 x≡ 1 is used to solve fully the equation 9sin 2 x 21sinx = 3cos 2 x 12 The second video explores how a graphical calculator can be used to find solutions of the equation by plotting both sides of the equation we are trying to solve, andThe key Pythagorean Trigonometric identity are sin 2 (t) cos 2 (t) = 1 tan 2 (t) 1 = sec 2 (t) 1 cot 2 (t) = csc 2 (t) So, from this recipe, we can infer the equations for different capacities additionally Learn more about Pythagoras Trig Identities Dividing through by c 2 gives a 2/ c 2 b 2/ c 2 = c 2/ c 2 This can be simplifiedTan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos 2 (x) sin 2 (x) = 2 cos 2 (x) 1 = 1 2 sin 2 (x) tan(2x) = 2 tan(x) / (1




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube
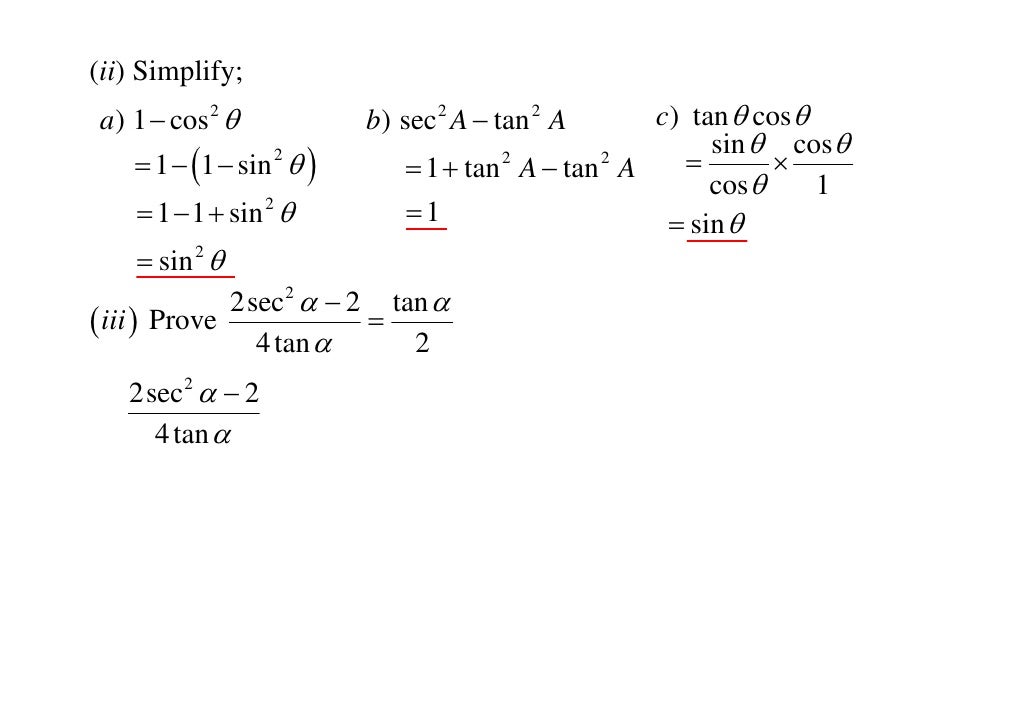



11 X1 T04 03 Pythagorean Trig Identities 10
Trigonometric functions can have several solutions Sine, cosine and tangent all have different positive or negative values depending on what quadrant they are in We have certain trigonometric identities Like sin 2 θ cos 2 θ = 1 and 1 tan 2 θ = sec 2 θ etc Such identities are identities in the sense that they hold for all value of the angles which satisfy the given condition among them and they are called conditional identities Trigonometric Identities With Examples Example 1 Prove the following trigonometric identities (i) (1 – sin 2Trig identities tan^2Section 71 Solving Trigonometric Equations and Identities 413 Try it Now 2 Solve 2 2sin ( ) 3cos(t t ) for all solutions t 0 2 In addition to the Pythagorean identity, it is often necessary to rewrite the tangent, secant,Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2 π while tangent and cotangent have period π Identities for negative




List Of Trigonometric Identities Wikipedia




Trigonometry Reciprocal Functions Ii Kus Objectives Bat Prove
The Pythagorean Identities are based on the properties of a right triangle cos2θ sin2θ = 1 1 cot2θ = csc2θ 1 tan2θ = sec2θ The evenodd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle tan(− θ)Tan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan(2x) = 2 tan(x) / (1 Here we will prove the problems on trigonometric identities As you know that the identity consists of two sides in equation, named Left Hand Side (abbreviated as LHS) and Right Hand Side (abbreviated as RHS)To prove the identity, sometimes we need to apply more fundamental identities, eg $\sin^2 x \cos^2 x = 1$ and use logical steps in order to lead one




Trigonometry Identities And Equations Ppt Download




Lesson 5 2 Verifying Trigonometric Identities By Griffin Heier
62 Trigonometric identities (EMBHH) An identity is a mathematical statement that equates one quantity with another Trigonometric identities allow us to simplify a given expression so that it contains sine and cosine ratios only This enables us to solve equations and also to prove other identities Quotient identity Quotient identity Complete the table without using a calculator,Identities expressing trig functions in terms of their supplements Sum, difference, and double angle formulas for tangent The half angle formulas The ones for sine and cosine take the positive or negative square root depending on the quadrant of the angle θ/2 For example, if θ/2 is an acute angle, then the positive root would be used Truly obscure identities These are just here forThe addition formulae and trigonometric identities are used to simplify or evaluate trigonometric expressions Trigonometric equations are solved using a



What Are The Quotient Identities For A Trigonometric Functions Socratic



2
Section 71 Solving Trigonometric Equations and Identities 413 Try it Now 2 Solve 2 2sin ( ) 3cos(t t ) for all solutions t 0 2 In addition to the Pythagorean identity, it is often necessary to rewrite the tangent, secant,Trig Identities for Calc 2 test one STUDY Flashcards Learn Write Spell Test PLAY Match Gravity Created by Liam_Wilcox Terms in this set (17) Basic Trig Identities for sin and cos sin^2(x)cos^2(x)=1 Basic Trig identities for tan and sec tan^2(x)1=sec^2(x) cot^2(x)1=csc^2(x) sin(AB) sin(2A) sin(AB)= sin(A)cos(B)cos(A)sin(B) sin(2A)=Trig identities or a trig substitution mcTYintusingtrig091 Some integrals involving trigonometric functions can be evaluated by using the trigonometric identities These allow the integrand to be written in an alternative form which may be more amenable to integration




Worksheet On Trigonometric Identities Establishing Identities Hints




Trigonometric Identities A Plus Topper
Some Useful Trigonometric Identities An identity is an equation whose left and right sides when defined are always equal regardless of the values of the variables the two sides contain Some very useful trigonometric identities are shown below The Pythagorean Identities $$\begin{array}{c} \cos^2 \theta \sin^2 \theta = 1\\ 1 \tan^2 \theta = \sec^2 \theta\\ 1 \cot^2 \theta = \csc^2There are lots more but not all angles have exact expressions involving nothing more than squareroots Which angles do?Following table gives the double angle identities which can be used while solving the equations You can also have #sin 2theta, cos 2theta# expressed in terms of #tan theta # as under #sin 2theta = (2tan theta) / (1 tan^2 theta)# #cos 2theta = (1 tan^2 theta) / (1 tan^2 theta)#




5 1 Fundamental Trig Identities Reciprocal Identities Sin




Derivatives Of Trigonometric Functions




Trig Identities Maple Learn Maplesoft



A Trig Identity




Basic Trigonometric Identities Class 10 Maths Formula Teachoo



Verifying Trigonometric Identities How To Do It The Easy Way Lesson Plan Spiral




How Do You Verify The Identity Tan2theta 2 Cottheta Tantheta Socratic




S A T C Trigonometry Applying Astc Reference Coterminal Angles Ppt Video Online Download



Ilectureonline




Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions



Trigonometry Identities




What Does It Mean To Prove A Trigonometric Identity Socratic




Tan 2x Formula What Is Tan 2x Formula Examples




Tangent Half Angle Formula Wikipedia




Solved 2 Prove The Following Trig Identities A Prove Tan Chegg Com



Proving Simplifying Using Trig Identities Lessons Blendspace



How To Prove Quotient And Reciprocal Identities Studypug



How I Remember Trig Identities Part 2 Beyond Solutions
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities




Trigonometric Identities Sin 2 X Cos 2 X Tan 2 X Youtube




Cos Sin Tan Csc Sec Cot
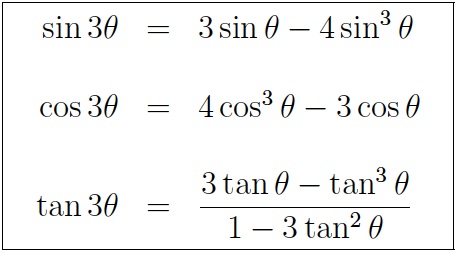



Summary Of Trigonometric Identities
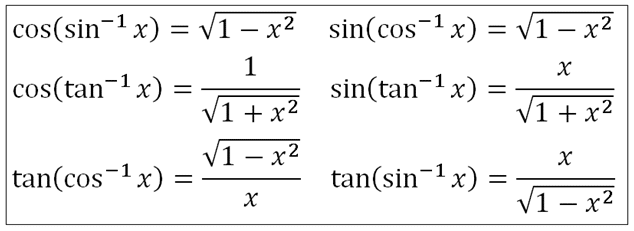



Inverse Trig Identities Reciprocal Of Trigonometric Function Trig




Trig Identities Bingo Card
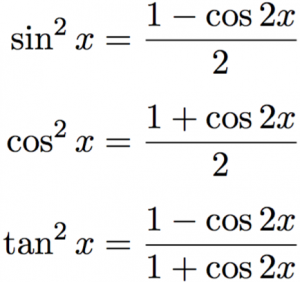



上 Tan2x Identity ただの悪魔の画像



Solved Trig Identities 1 Sin Cos 2 Sin Cos 2 2 2 Tan2 Cos2 Cot2 Sin2 1 3 Sec Course Hero




Chapter 7 Trigonometric Identities And Equations Jami Wang




Solved Inquiry 11 8 Marks Prove The Following Trig Chegg Com



2




Trigonometric Identities




Lesson 22 Trigonometric Identities Ib Math Hl
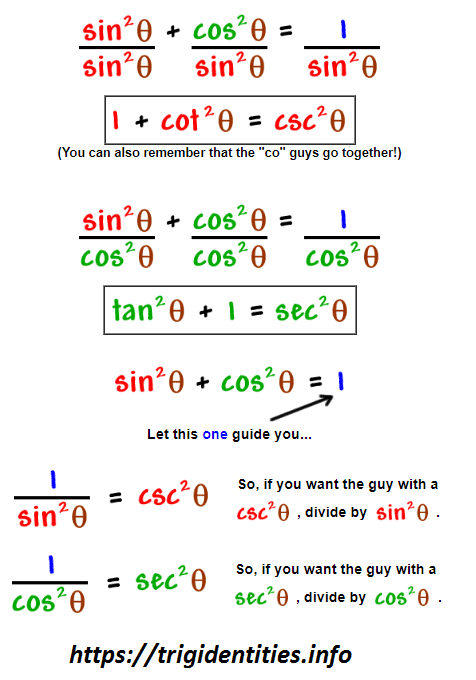



Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities



1



2




Trigonometric Identities List Of Trigonometric Identities Examples
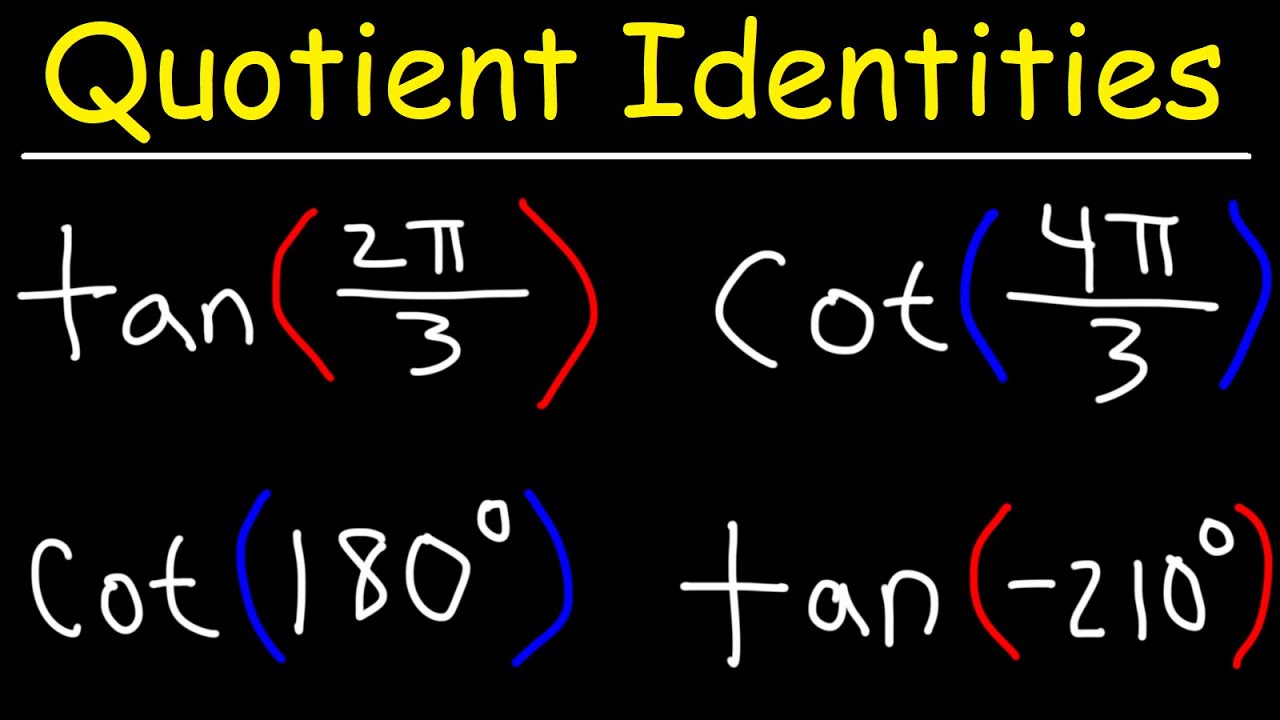



Quotient Identities Evaluating Tangent And Cotangent Functions Youtube



最も人気のある Tan2 Identity ただの悪魔の画像




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X 1 Ppt Powerpoint




Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube




Solved 2 Prove The Following Trig Identities A Prove Tan Chegg Com




Chapter 7 Trigonometric Identities And Equations Ppt Download




Integrate Sec 2x Method 1




Cos 2x Formula Derivation Examples What Is Cos 2a Formula




Trigonometric Identities A Plus Topper



Tan2x ただの悪魔の画像
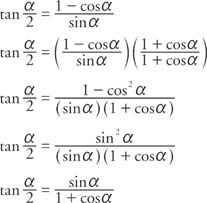



Tangent Identities
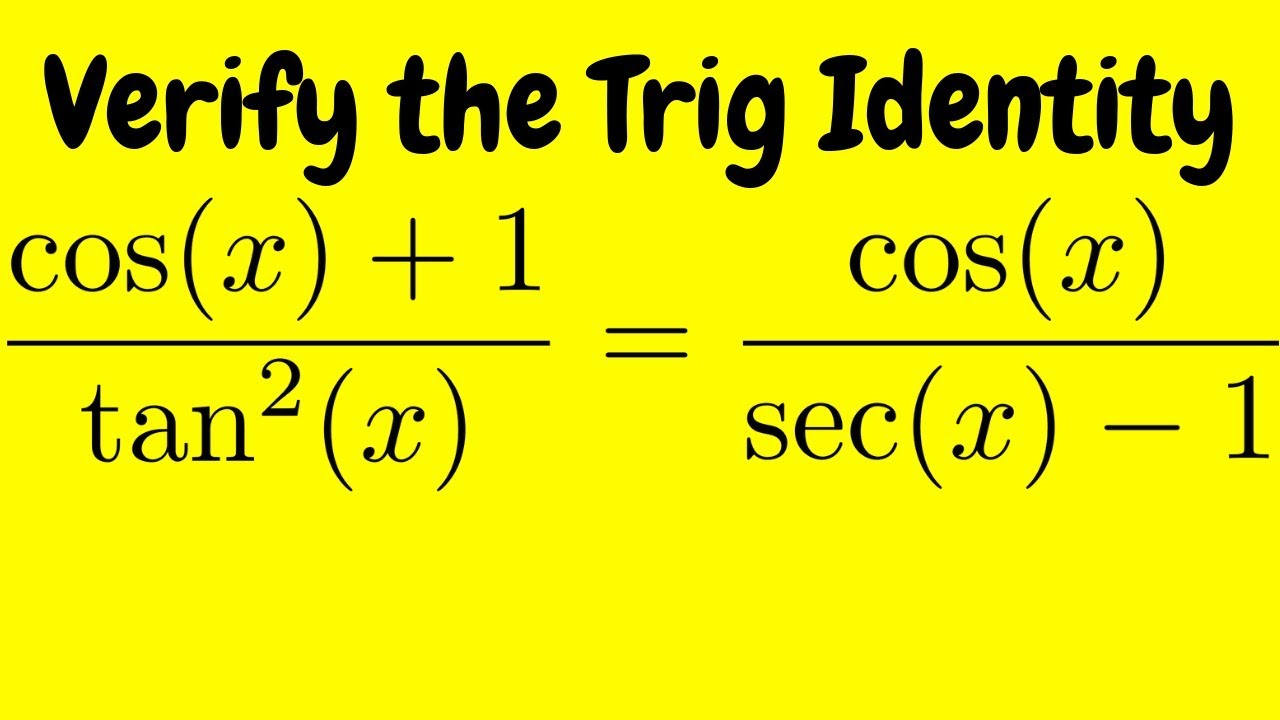



Verifying A Trigonometric Identity Cos X 1 Tan 2 X Cos X Sec X 1 Youtube




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




Solved We Wish To Prove The Following Trig Identity Tan X Chegg Com




Summary Of Trigonometric Identities
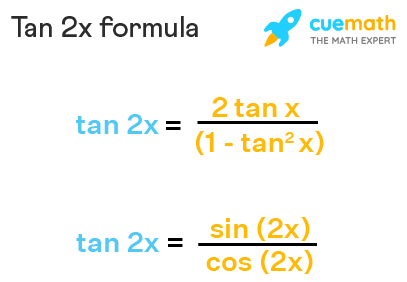



Tan 2x Formula What Is Tan 2x Formula Examples




How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic
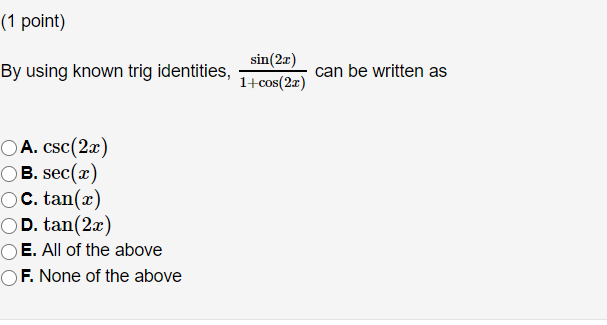



Solved 1 Point By Using Known Trig Identities Sin 2 Chegg Com




4 1 Revision Trigonometry Siyavula



What Is The Formula Of Tan2x Quora




Example 1 Verify A Trigonometric Identity The Left Hand Side Of This Identity Is More Complicated So Transform That Expression Into The One On The Right Ppt Download



1
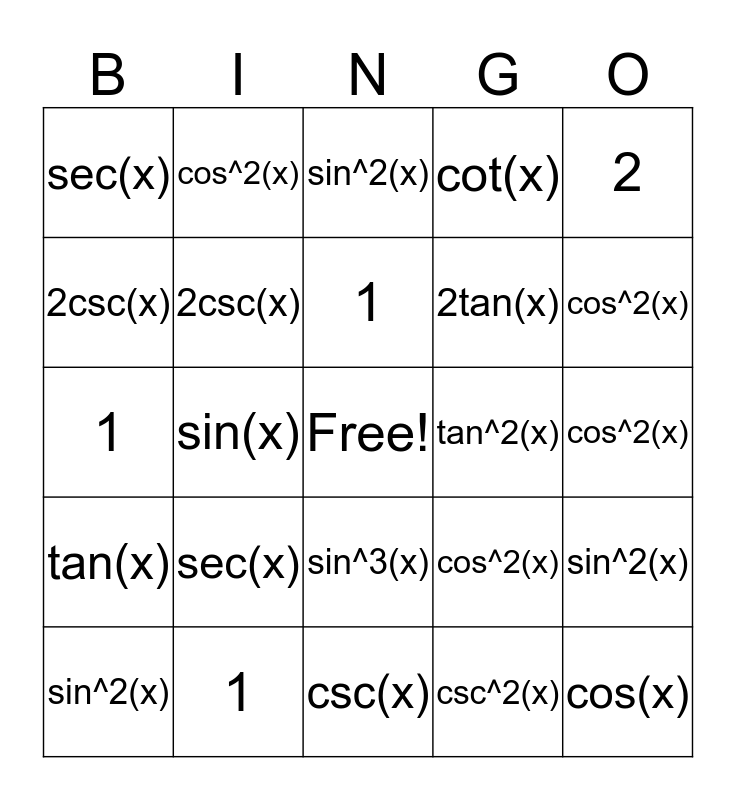



Trig Identities Bingo Card




Trigonometric Identities December 10 Remember Y Sin




Pythagorean Trig Identities Recall Pythagoras Theorem Trig Identities
x-1=sec(squared)x.jpg)



10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com
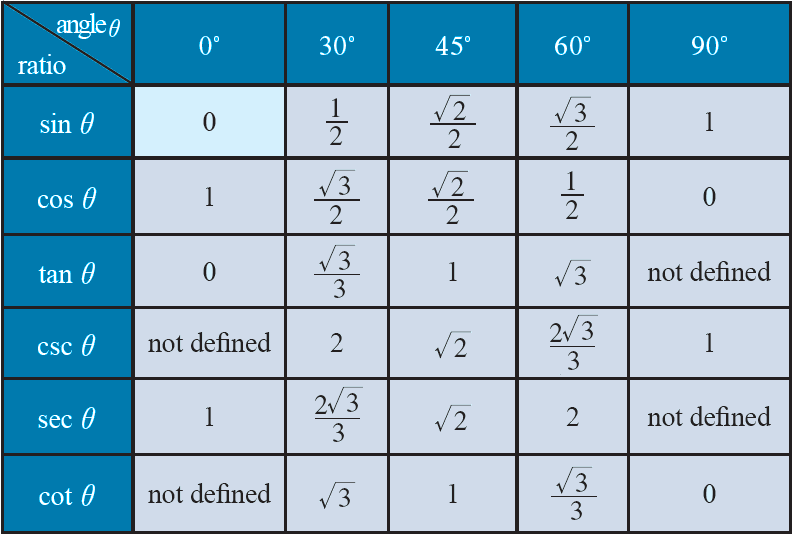



Trigonometric Identities




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download
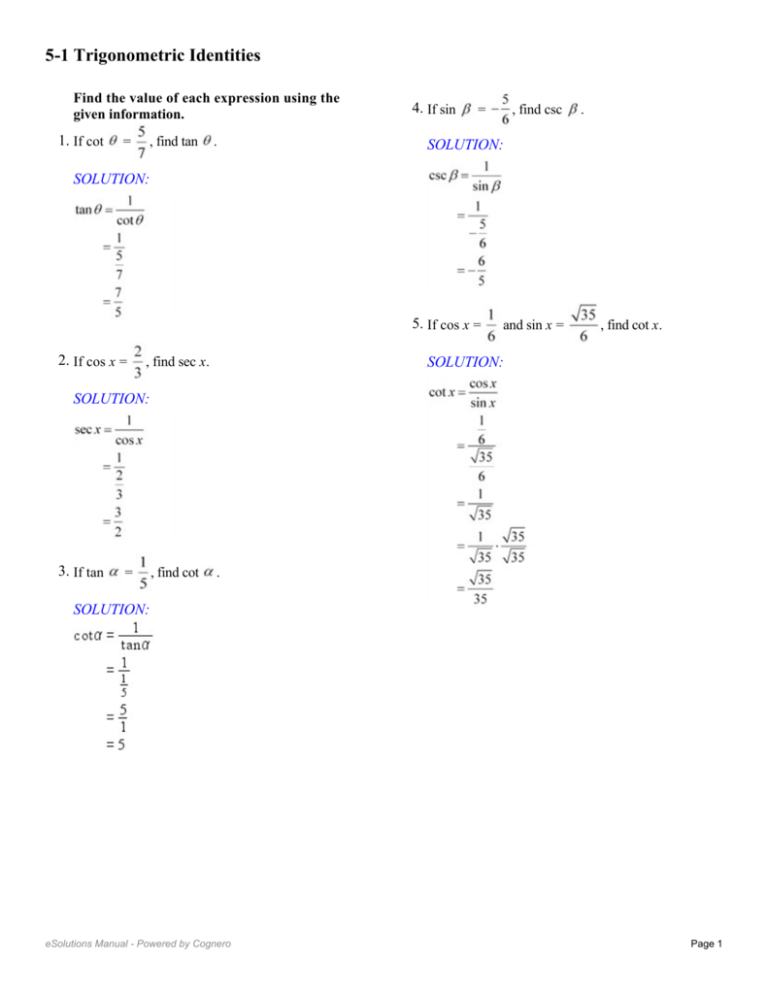



5 1 Trigonometric Identities
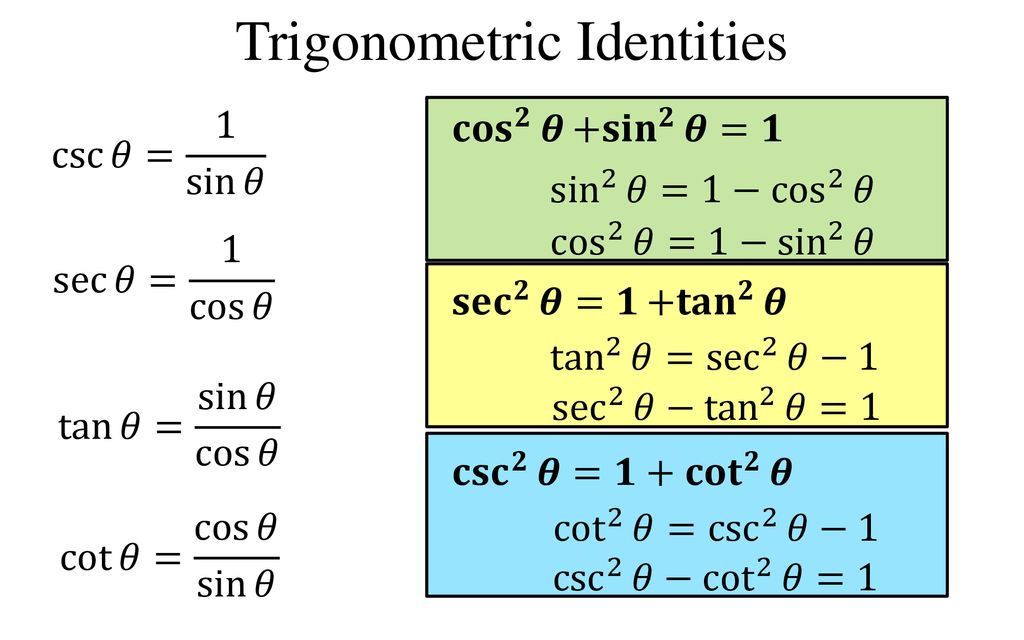



Trigonometric Identities And Equations Ppt Download



Cos2x Identity




Analytic Trig Ppt Video Online Download



1



7 Proving Ids Trig Functions Identities



Solved Prove The Following Trig Identity Sec 2 X 2secx Cosx Cos 2 X Tan 2 X Sin 2 X Course Hero
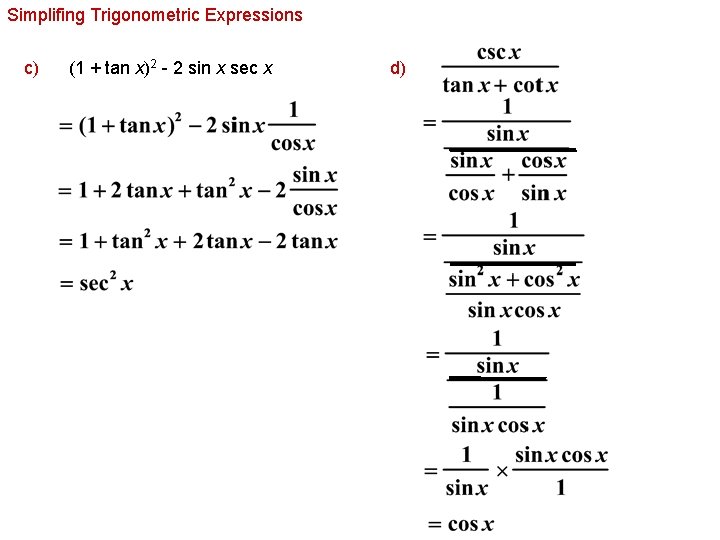



While You Wait Trigonometric Identities And Equations Section




Solved We Wish To Prove The Following Trig Identity Cos 2 Chegg Com




Trigonometric Identities List Of Trigonometric Identities Examples




Summary Of Trigonometric Identities




Trigonometric Identities And Examples With Worksheets




Lesson Video Evaluating Trigonometric Functions Using Pythagorean Identities Nagwa




Tangent Identities




Solved Inquiry 11 8 Marks Prove The Following Trig Chegg Com




Trigonometric Identities Ml Aggarwal Solutions Icse Class 10 Icsehelp




Trig Identities For Pre Calculus Dummies




5 2 Verifying Trigonometric Identities Copyright Cengage Learning
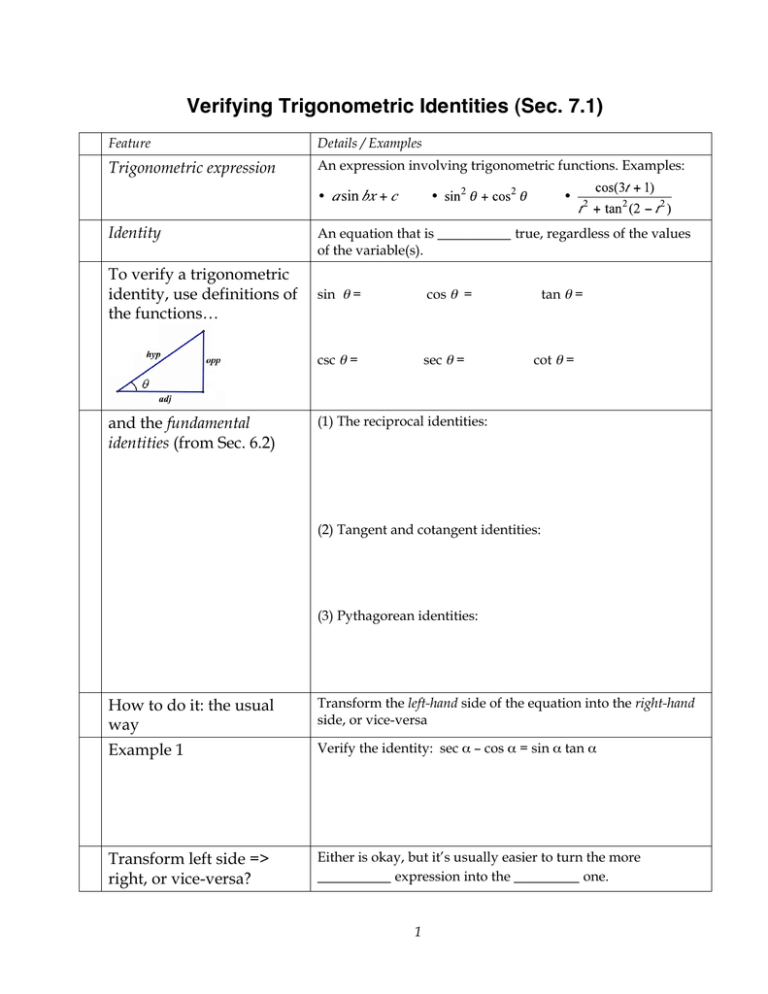



Verifying Trigonometric Identities Sec 7 1 Trigonometric Expression Identity




bestpictjcry Tan 2x Tan 2x



Trigonometric Identities All In One Cheat Sheet Docsity



1



0 件のコメント:
コメントを投稿